Bibliothek für das Grundpraktikum¶
Die Praktikumsbibliothek stellt grundlegende Funktionen, die bei der Datenanalyse im Grundpraktikum verwendet werden, und Hilfsmittel zum Einlesen der mit dem Cassy-System aufgezeichneten Messdaten zur Verfügung. Sie richtet sich an alle Teilnehmer des Grundpraktikums Physik für Physiker und Mathematiker an der RWTH Aachen. Als Programmiersprache wurde python gewählt, wegen des einfachen Zugangs, der weiten Verbreitung als Analysewerkzeug in der Physik und als Anknüpfung zu dem in der Vorlesung zur Datenverarbeitung vermittelten Wissen. Die python-Versionen 3.x werden unterstützt.
Bitte melden Sie Feedback, Probleme und Anregungen an Henning Gast.
Installation der Praktikumsbibliothek¶
Die Praktikumsbibliothek kann ganz einfach mit pip installiert werden. Unter Linux oder MacOS führt man den folgenden Befehl in einem Terminal aus. Benutzt man eine Anaconda-Installation unter Windows, drücke man die Windows-Taste und suche dann nach dem Programm „Anaconda Prompt“. Dort gibt man den folgenden Befehl ein (hier typischerweise ohne „–user“):
pip install --user praktikum
Ein Satz von Beispielen zur Praktikumsbibliothek kann hier (als zip-Datei) bzw. hier (als Tarball) heruntergeladen werden. Nach dem Entpacken der heruntergeladenen Datei finden Sie im Unterverzeichnis „Beispiele“ einige Beispiel-Skripte und die zugehörigen Cassy-Dateien, die die Verwendung der wesentlichen Teile der Praktikumsbibliothek illustrieren sollen. Es wird dringend empfohlen, dass Sie die Beispiel-Skripte vor dem ersten Versuchstag einmal ausprobieren, um sicherzustellen, dass Ihre python-Installation und die Praktikumsbibliothek funktionieren. Sie sollten auch den Gang der Analyse in den Beispielen nachvollziehen.
Die folgenden Python-Module werden benötigt: numpy, scipy, matplotlib und uncertainties. Sie werden von pip automatisch installiert, falls sie nicht schon vorhanden sind.
Einlesen von Cassy-Daten¶
Die während der Versuchsausführung mit Cassy gewonnenen Messdaten sollen auf einem USB-Stick gespeichert und dann zu Hause ausgewertet werden.
cassy_info¶
Um zunächst einen Überblick über die in einer Cassy-Datei gespeicherten Messungen zu erhalten, verwendet man das Skript cassy_info:
cassy_info Beispiele/lab/Pendel.lab
Beispiel für die Ausgabe:
Lese CASSY-1 Textdatei: Beispiele/lab/Pendel.lab
Messung #1: (Datenreihen: n, t, U_A1, U_B1, f_1)
Index n 16001 Werte von 1 bis 16001
Zeit t/s 16001 Werte von 0 bis 160
Spannung U_A1/V 16001 Werte von 0.342 bis 0.7725
Spannung U_B1/V 16001 Werte von -1.11 bis -1.068
neue Größe f_1/V (leer)
Über die auch während der Messungen von Cassy verwendeten Symbole („U_A1“, „U_B1“, „f“, usw.) greift man dann später auf die Datenreihen zu.
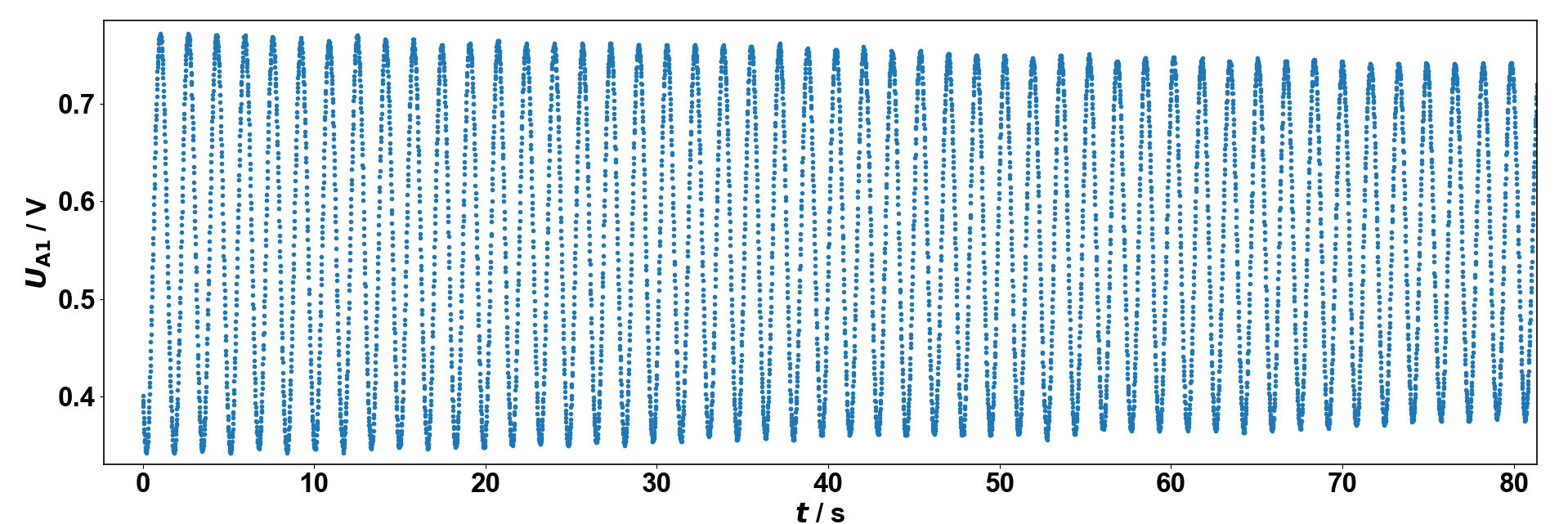
cassy_plot¶
Mit dem Skript cassy_plot kann man schnell eine grafische Auftragung von zwei Datenreihen erzeugen:
cassy_plot Beispiele/lab/Pendel.lab t U_A1
Analyse der Cassy-Daten¶
Im Folgenden betrachten wir an einem einfachen Beispiel, der
Vermessung eines Ohmschen Widerstands mit Hilfe des Ohmschen Gesetzes
\(U=RI\), den typischen Gang einer Analyse von Cassy-Daten mit
der Praktikumsbibliothek. Die verwendete Cassy-Datei und das
Analyse-Skript sind in den Beispielen zur Praktikumsbibliothek zu
finden (Beispiele/Beispiel_Widerstand.py).
Zu Beginn werden die notwendigen Module geladen:
#! /usr/bin/env python3
# -*- coding: utf-8 -*-
from praktikum import analyse
from praktikum import cassy
import numpy as np
import matplotlib.pyplot as plt
from uncertainties import ufloat
Wir passen einige Parameter für das Layout an, um eine gut lesbare und ausreichend große Beschriftung der Achsen sowie nicht zu dünne Linien zu erhalten:
plt.rcParams['font.size'] = 24.0
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = 'Arial'
plt.rcParams['font.weight'] = 'bold'
plt.rcParams['axes.labelsize'] = 'medium'
plt.rcParams['axes.labelweight'] = 'bold'
plt.rcParams['axes.linewidth'] = 1.2
plt.rcParams['lines.linewidth'] = 2.0
Jetzt besorgen wir uns die relevanten Messreihen:
inputfile = 'labx/widerstand.labx'
data = cassy.CassyDaten(inputfile)
# Es gibt nur eine einzige Messung in der Datei.
U = data.messung(1).datenreihe('U_B1').werte
I = data.messung(1).datenreihe('I_A1').werte
Mithilfe unserer Aufzeichnungen rechnen wir aus den verwendeten Messbereichen die Messunsicherheiten aus:
# Messbereich -> Digitalisierungsfehler (Cassy-ADC hat 12 bits => 4096 mögliche Werte)
sigmaU = 20.0 / 4096. / np.sqrt(12.) * np.ones_like(U)
sigmaI = 0.2 / 4096. / np.sqrt(12.) * np.ones_like(I)
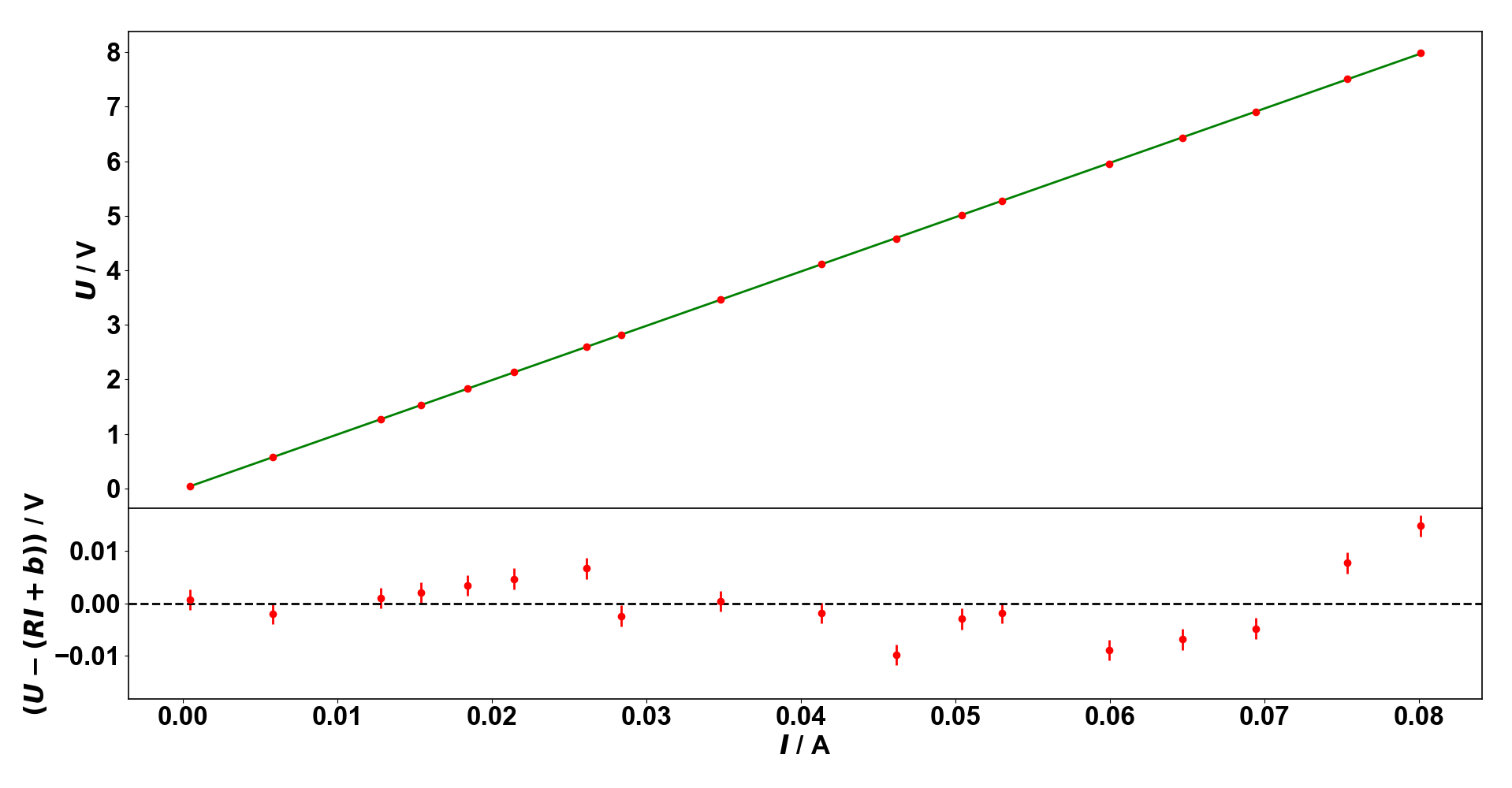
Wir wollen die Rohdaten grafisch auftragen und anschließend eine lineare Regression der Spannungskurve als Funktion des Stroms durchführen, einschließlich eines Residuenplots.
Zunächst erstellen wir eine leere Abbildung und unterteilen sie in zwei Hälften, dann zeichnen wir in die obere Hälfte die Rohdaten:
# Erstelle eine schön große Abbildung mit zwei Achsenpaaren (oben für die Messdaten samt angepasster Gerade,
# unten für den Residuenplot. Die x-Achse teilen sich beide Plots. Als Höhenverhältnis verwenden wir 5:2.
fig, ax = plt.subplots(2, 1, figsize=(20,10), sharex=True, gridspec_kw={'height_ratios': [5, 2]})
# Grafische Darstellung der Rohdaten
ax[0].errorbar(I, U, xerr=sigmaI, yerr=sigmaU, color='red', fmt='o')
ax[0].set_xlabel('$I$ / A')
ax[0].set_ylabel('$U$ / V')
Jetzt führen wir die lineare Regression durch, geben das Ergebnis aus und zeichnen die Anpassungsgerade in unseren Plot mit ein:
R, eR, b, eb, chiq, corr = analyse.lineare_regression_xy(I, U, sigmaI, sigmaU)
uR = ufloat(R, eR)
ub = ufloat(b, eb)
dof = len(I) - 2
print(f'R = ({uR}) Ohm, b = ({ub}) V, chi2/dof = {chiq:.1f} / {dof}, corr = {corr:g}')
ax[0].plot(I, R*I+b, color='green')
Schließlich erstellen wir den Residuenplot:
# Für den Residuenplot werden die Beiträge von Ordinate und Abszisse (gewichtet mit der Steigung) quadratisch addiert.
sigmaRes = np.sqrt((R*sigmaI)**2 + sigmaU**2)
# Zunächst plotten wir eine gestrichelte Nulllinie, dann den eigentlichen Residuenplot:
ax[1].axhline(y=0., color='black', linestyle='--')
ax[1].errorbar(I, U-(R*I+b), yerr=sigmaRes, color='red', fmt='o')
ax[1].set_xlabel('$I$ / A')
ax[1].set_ylabel('$(U-(RI+b))$ / V')
# Wir sorgen dafür, dass die y-Achse beim Residuenplot symmetrisch um die Nulllinie ist:
ymax = max([abs(x) for x in ax[1].get_ylim()])
ax[1].set_ylim(-ymax, ymax)
Finales Layout:
plt.tight_layout()
fig.subplots_adjust(hspace=0.0)
Am Ende wollen wir die Abbildung noch interaktiv bearbeiten können:
plt.show()
Nützliche Hilfsmittel¶
Für die Erstellung von grafischen Darstellungen der Daten (Graphen, Histogramme, Residuenplots, etc.) soll im Praktikum matplotlib verwendet werden. Die am häufigsten im Praktikum benötigten Plots und Befehle werden in den Beispiel-Skripten verwendet.
Hinweise für gute Plots:
Um Plots mit gut leserlichen Achsenbeschriftungen zu erzeugen, muss
man ggfs. die Standardeinstellungen von matplotlib anpassen. Das geht
am einfachsten, indem man die Konfigurationsdatei matplotlibrc von
matplotlib editiert. Um herauszufinden, in welchem Verzeichnis sie
sich befindet, führt man den folgenden Befehl aus:
python -c 'import matplotlib as mpl; print(mpl.get_configdir())'
Um zum Beispiel die Standardschriftgröße auf 16pt zu setzen, fügt man die folgende Zeile ein, bzw. editiert einen schon vorhandenen Eintrag:
font.size : 16.0
Beim Abspeichern der mit matplotlib erzeugten Plots ist es wichtig, ein dem Zweck angepasstes Dateiformat zu wählen: Um einen Plot für eine Präsentation zu erzeugen, speichere man ihn als hochauflösende png-Datei. Um einen Plot für das Protokoll zu erzeugen, speichere man ihn als Vektorgrafik (eps oder pdf).